Desafio - Análise Combinatória
UM AUTOMÓVEL COMPORTA DOIS PASSAGEIROS NO BANCO DA FRENTE E TRÊS NO BANCO DE TRÁS. CALCULE O NÚMERO DE ALTERNATIVAS DISTINTAS PARA LOTAR O AUTOMÓVEL UTILIZANDO 7 PESSOAS, DE MODO QUE UMA DESSAS PESSOAS NUNCA OCUPE UM LUGAR NOS BANCOS DA FRENTE.
Desafio - Comentem o resultado
EU TENHO O DOBRO DA IDADE QUE TU TINHAS QUANDO EU TINHA A TUA IDADE. QUANDO TU TIVERES A MINHA IDADE, A SOMA DAS NOSSAS IDADES SERÁ DE 45 ANOS. QUAIS SÃO AS NOSSAS IDADES???
Enquanto você pensa em pizza, eu descubro a sua idade!
• Primeiro de tudo, pense no número de vezes por semana que você sente vontade de comer pizza (tente pensar em mais de uma vez, mas menos que dez);
• Multiplique esse número por 2;
• Some 5;
• Multiplique o resultado por 50;
• Se você já fez aniversário este ano, some 1762, se ainda não fez, some 1761;
• Agora, subtraia os quatro dígitos do ano que você nasceu do resultado que obteve;
• Você deve ter obtido um resultado de três dígitos...
• O primeiro dígito desse resultado foi seu número original (o número de vezes que você pensa em comer pizza na semana).
• Os dois últimos números são SUA IDADE!!!
Repetição do númeor 6174
Escolha um número de 4 dígitos (exceto os números 1111, 2222, etc) e faça o seguinte:
1) Coloque os seus dígitos em ordem crescente
2) Coloque os seus dígitos em ordem decrescente
3) Subtraia o número menor do número maior
2) Coloque os seus dígitos em ordem decrescente
3) Subtraia o número menor do número maior
Repita os passos 1, 2 e 3 para o resultado, e assim por diante. O que acontece?
Vamos tentar com o número 8415.
Dígitos em ordem crescente: 1458
Dígitos em ordem decrescente: 8541
Subtraindo o menor do maior: 8541 - 1458 = 7083
Repetindo o processo com o número 7083:
8730 - 0378 = 8352
8532 - 2358 = 6174
7641 - 1467 = 6174
7641 - 1467 = 6174
7641 - 1467 = 6174 (a repetição continua....)
Dígitos em ordem decrescente: 8541
Subtraindo o menor do maior: 8541 - 1458 = 7083
Repetindo o processo com o número 7083:
8730 - 0378 = 8352
8532 - 2358 = 6174
7641 - 1467 = 6174
7641 - 1467 = 6174
7641 - 1467 = 6174 (a repetição continua....)
Incrivelmente, todos os números de 4 dígitos que não são múltiplos de 1111 acabam caindo nessa repetição.
O traço no meio do sete
Muitas pessoas, ao escreverem o numero 7, ainda colocam um pequeno traço no meio do número. Oficialmente, este pequeno traço não existe, como podemos perceber nos teclados dos computadores ou calculadoras. Mas qual é a origem deste costume?
Para melhor entender as diferentes grafias do número 7, deve-se lembrar que nosso sistema é originário do sistema indo-arábico. Existe a teoria de que o formato destes números está relacionado à quantidade de ângulos que possuem, como mostra a figura abaixo (o 1 possui 1 ângulo, o 2 possui 2 ângulos...). Assim, o traço seria necessário para realizar a diferenciação.
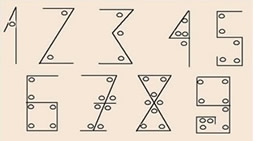
O traço do sete ainda é um recurso utilizado nas escolas para que os alunos das séries iniciais diferenciem sua forma da escrita do número 1. O mesmo recurso é utilizado em atividades relacionadas à informática, para orientar os digitadores na diferenciação do "zero" em relação à letra "O". No zero, é colocado um traço interno na diagonal.
Como quantificar pessoas em lugares públicos
Conhecer a quantidade de pessoas em um determinado local é importante para o Poder Público, pois assim poderá planejar o policiamento, estimar a necessidade real de profissionais das diversas áreas - médicos, enfermeiros, bombeiros, infra-estrutura, e ainda, quantidade de copos de água, ambulância e outros benefícios.
Este cálculo é fácil de fazer, bastando para isso uma simples operação matemática. Sabe-se que um metro quadrado (m²) pode ser ocupado por nove pessoas, no máximo, nas grandes concentrações.
As concentrações são divididas em três categorias: pequena, média e grande. Na concentração pequena, calculam-se três pessoas por metro quadrado; na média, seis pessoas; e na grande nove pessoas por metro quadrado.
Multiplicando-se o número médio de participantes por m² pela área útil ocupada, chegar-se-á ao número médio de pessoas presentes numa reunião. Eis a regra:
N P m² x A (m²) = T P A
Sendo:
N P m² = número de pessoas por m²;
A = área ocupada em m²;
T P A = Número total de pessoas na área.
N P m² = número de pessoas por m²;
A = área ocupada em m²;
T P A = Número total de pessoas na área.
Exemplo hipotético: O cantor Roberto Carlos fará um show em um espaço livre de 100 metros de comprimento por 60 metros de largura. Qual a capacidade de espectadores em pé neste local?
Temos os seguintes dados:
Número de pessoas por metro quadrado = 9
Area quadrada do local? 100 x 60 = 6000 m²
Número de pessoas por metro quadrado = 9
Area quadrada do local? 100 x 60 = 6000 m²
Resolvendo o problema 9 x 6000 = 54000.
Logo, 54000 é o número máximo de pessoas em pé que o local comporta.
Com apenas um olhar você pode ter o público aproximado. Se a quantidade de pessoas for como a de uma decisão de campeonato de futebol, multiplica-se a área quadrada por nove. Se você achar que tem muita gente, mas percebe muito espaço vazio, multiplique por 6. E assim sucessivamente.
A curiosa espiral de números primos
A espiral de números primos, também conhecida como Espiral de Ulam, é uma representação gráfica na qual os inteiros positivos são dispostos em forma de espiral, com os números primos sendo indicados de alguma forma ao longo dessa espiral.
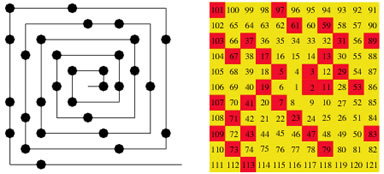
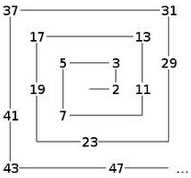
Foi descoberta pelo matemático Stanislaw Ulam em 1963, enquanto rabiscava num papel, por estar entediado durante um encontro científico. Ele verificou que os números assinalados tendiam a agrupar-se segundo diagonais. Conforme imagem abaixo, onde os números primos estão assinalados em preto, as diagonais são perfeitamente visíveis, confirmando o padrão, que ainda permanece por explicar.
O que é a medalha Fields?
Trata-se de uma medalha concedida para pessoas que fizeram contribuições relevantes para as ciências matemáticas. Também conhecida como "Medalha Internacional de Descobrimentos Proeminentes em Matemática", a Medalha Fields é concedida a cada quatro anos, no Congresso Internacional da União Internacional de Matemática (IMU), a dois, três ou quatro matemáticos, normalmente com até 40 anos de idade. Para muitos, é a maior honra que um matemático pode receber, sendo comparada com um "Prêmio Nobel".
A primeira medalha foi entregue em 1936, para o matemático finlandês Lars Ahlfors e o matemático norte-americano Jesse Douglas. A ideia é reconhecer e apoiar jovens pesquisadores matemáticos, que contribuiram de forma significativa para este campo da ciência. Em 2014, o brasileiro Artur Ávila tornou-se o primeiro matemático da América Latina a ser condecorado com a Medalha Fields.
|
Você conhece o número mágico?
Escolha um número de 4 dígitos (exceto os números 1111, 2222, etc) e faça o seguinte:
1) Coloque os seus dígitos em ordem crescente
2) Coloque os seus dígitos em ordem decrescente
3) Subtraia o número menor do número maior
2) Coloque os seus dígitos em ordem decrescente
3) Subtraia o número menor do número maior
Repita os passos 1, 2 e 3 para o resultado, e assim por diante. O que acontece?
Vamos tentar com o número 8415.
Dígitos em ordem crescente: 1458
Dígitos em ordem decrescente: 8541
Subtraindo o menor do maior: 8541 - 1458 = 7083
Repetindo o processo com o número 7083:
8730 - 0378 = 8352
8532 - 2358 = 6174
7641 - 1467 = 6174
7641 - 1467 = 6174
7641 - 1467 = 6174 (a repetição continua....)
Dígitos em ordem decrescente: 8541
Subtraindo o menor do maior: 8541 - 1458 = 7083
Repetindo o processo com o número 7083:
8730 - 0378 = 8352
8532 - 2358 = 6174
7641 - 1467 = 6174
7641 - 1467 = 6174
7641 - 1467 = 6174 (a repetição continua....)
Incrivelmente, todos os números de 4 dígitos que não são múltiplos de 1111 acabam caindo nessa repetição.
Assinar:
Postagens (Atom)